Pretzangles

 

For thousands of years people in all cultures have been fascinated by geometrical patterns for use in decorative and religious arts. These patterns can be split into two broad categories:

 

1 Tilings (Tessellations). Here the main aim is to fill space – a floor or a wall – with an interesting pattern. You can, if you wish, fill the space with a single repeating motif, but your choice is limited to triangular, square or hexagonal tiles. If you want to use regular polygons then the 11 Archimedean tilings (12 if you count enantiomers) are the classical examples. But many interesting tilings can be produced with irregular shapes. The complex tilings of MC Escher are nothing new – examples exist in many ancient cultures.

 

2 Interlacings. Simple interlacings are again universal. But most people think of the wonders of Celtic knotwork as the prime examples of beautiful interlacings. The Islamic tradition of geometrical art has a different sort of beauty and complexity and blends together tilings and interlacings in an endless variety of forms.

 

Although tilings and interlacings are closely interlinked, mathematicians tend to study them via different means. Tilings and patterns (the title of the indispensable book by Grünbaum & Shephard) tend to have one form of literature and interlacings tend to come under knot theory (see Peter Suber’s Knots on the Web site for all the information you could wish for).

 

Of course there are good reasons for some sort of separation. Many interlacing designs head off into regions of fluid shapes that would never make useful tessellations. And the need to cover large areas of space mean that those interested in tilings tend not make use of much of the world of knot theory.

 

When it comes to practical workers in arts and crafts, the mathematical theories become a distant background, and it becomes very easy to forget that tilings and interlacings are closely related.

 

Moreover, the challenge of producing even a moderately complex tiling or an interlacing soon becomes too much for most of us. It’s one thing to say that the maths of the Archimedean tilings of the plane is simple; it’s another thing to actually produce an effective tiling. The knot theory behind a moderately complex interlacing may be easy for the knot theorist, but actually making such a knot is highly challenging.

 

With modern computer power it might seem easy to rectify the situation. And of course many excellent programs exist to create pure mathematical tilings or knots.

 

Yet these programs are usually too mathematical for the practical artist. The results are too perfect, a little sterile, and leave little room for that spark of creativity that brings a tiling or a knot to life.

 

Amateur programmers can step in at this point and create tools that are more practical. Quite a few programs allow users to stick together various tilings. Rather less programs exist that can create intricate knotwork designs. A typical example of the latter is Steve Abbott’s Computer Drawn Celtic Knotwork. Any user after a few hours practice can produce many intricate knots which can then be used as templates for lace making, wood carving, embroidery, tattoo design etc.

 

This last program is singled out for another reason. Tilings and interlacings work in 3 dimensions as well as 2. In Steve Abbott’s program, the move into the 3rd dimension is a modest one – it just brings the 2D knots out of the plane. But it’s a step in the right direction.

 

For tiling theory the move into the 3rd dimension turns out to be not immediately interesting. The same basic maths that demonstrates the 11 Archimedean tilings of the plane show that you can get 5 Platonic solids and 13 Archimedean solids by combining the various regular polygons. Creating these shapes in a program is trivial – you just calculate the coordinates and put them into any 3D program and you can look at these beautiful shapes, map textures onto them and … well, that’s about all you can do.

 

Pretzangles

The Pretzangles approach claims no new fundamental insights into tilings or interlacings. But it is a fresh approach to tiling and interlacing that provides a powerful tool for practical artists working in 2D and in 3D.

 

Whereas most approaches to tiling concentrate on tiling, and most approaches to interlacings concentrate on interlacing, the Pretzangles principle states that tilings and interlacings grow out of each other. The word ‘grow’ is significant. In Pretzangles you start with a Seed, such as a hexagon, to which you add some Shapes. You now place the Seeds and Shapes in some sort of regular pattern (2D or 3D) and a beautiful combination of tiling/interlace emerges spontaneously. Small changes in the Shapes within the Seeds bring large changes to form that emerges.

 

And just as a flower bed rarely looks good with just one type of seed, placing different Seeds and Shapes together starts to produce a rich garden of visual delights.

 

The vision behind Pretzangles started in 197X when Matthew’s nephew exclaimed in delight that a pattern of under-and-over had suddenly appeared in one of Matthew’s designs. Years of carefully studying this emergent behaviour convinced Matthew that he had a powerful new graphical tool. Long hours of careful craftsmanship (backed up by years of training as a Navy draftsman) produced elegant designs of great depth and beauty.

 

But sharing this vision with others proved difficult. Although everyone loved the designs, they were not able to grasp the power of the Pretzangles principle. In retrospect, it’s not really surprising. Like so much in tiling and interlacing, although the principle seems easy, realising it in practice is much harder. Not everyone has the skills to patiently draw regular sets of Seeds and Shapes, or the imagination to know which combinations might be the most effective.

 

Here’s a classic Pretzangle. It happens to be the same as the Crocker Bank logo.

 

You can see that it’s a Seed hexagon with a triangle drawn along each edge of the hexagon. The triangle is only drawn once – it is then copied around the other 5 sides.

 

Then came another moment of inspiration. By chance, Matthew discovered Steve’s Celtic knots program. More importantly, Matthew saw these knots in a way that other users never did: he saw them as tessellations of Seed/Shape combinations. Perhaps, he thought, Steve’s program already used the Pretzangles principle.

 

Here’s a comparison of the Pretzangle:

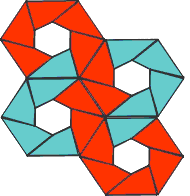
and the Celtic knot:

But the method behind the Celtic knots had no notion of Pretzangles. It was based on an entirely different approach. Even worse, when Matthew tried to explain the principle and sent examples of it, Steve just didn’t ‘get’ it. So even though Steve’s program produced ‘Pretzangle’ designs, neither the program nor its designer had any notion of the Pretzangle principle.

 

Then started a hectic stream of e-mails. The more Matthew tried to explain, the less Steve understood it. In one despairing e-mail, Steve tried to explain to Matthew why he didn’t ‘get’ the Pretzangle principle. But the act of writing the e-mail suddenly turned on the lightbulb and for the first time Matthew had someone else who ‘got’ the Pretzangle principle.

 

A very crude program was quickly written to confirm that a computerised Pretzangles program could work. The results astonished both; Pretzangles just leapt off the computer screen and the shear power of the approach started to appear.

 

Because the Pretzangles principle works equally in 3D, the program evolved to handle tiling and interlacing within the regular Platonic and Archimedean solids.

 

The program

It was a very long way from that crude prototype to the current version. In all the hard work needed to make the program, the only thing that didn’t change at all was the Pretzangle principle itself – and the prime need to combine power with ease of use.

 

Here’s what the program can do:

 

 

Surprises

The surprising thing about Pretzangles is that no two users seem to use it in the same way. Everyone has a different vision of how tilings and tessellations should grow. Some users tend to create precise ‘mathematical’ images. Others create designs of simple beauty. Others create wild complexity. Some users see their creations as animals or butterflies. Others seem them as if they were looking into a kaleidoscope.

 

But above all, users find they can create vibrant, complex forms that they can use in their own art or craft – be it painting or crochet or burning designs into wood.

 

And this is a vindication of the Pretzangles principle. Although the elements (tiling and interlacing) are not new, and although Pretzangles hold no surprises for the knowledgeable mathematician, the delicate balance between tiling and interlacing inherent in Pretzangles, and its extension in 2D and 3D makes it a unique power tool for all those who love to explore the interaction between art, craft mathematicsand computer design, and who love to expect the unexpected from this potent combination.

 

The Pretzangles program comes with a large gallery of files to help the user: the Archimedean tilings; the Platonic and Archimedean solids; tutorial examples from simple to complex; sample .emf and .wrl files. And of course it comes with a complete Help file.

 

The Pretzangles web community is creating a wealth of other Pretzangle designs for other Pretzanglers to use in their own way.

 

The program automatically adds the creator’s name (if he/she chooses) to the .prz file so that others know who deserves the credit for a given design.

 

Matthew Kells

Steven Abbott

 

Text Copyright © 2001 Matthew Kells

The Pretzangles name Copyright © 2000 Matthew Kells

Return to the Pretzangles homepage